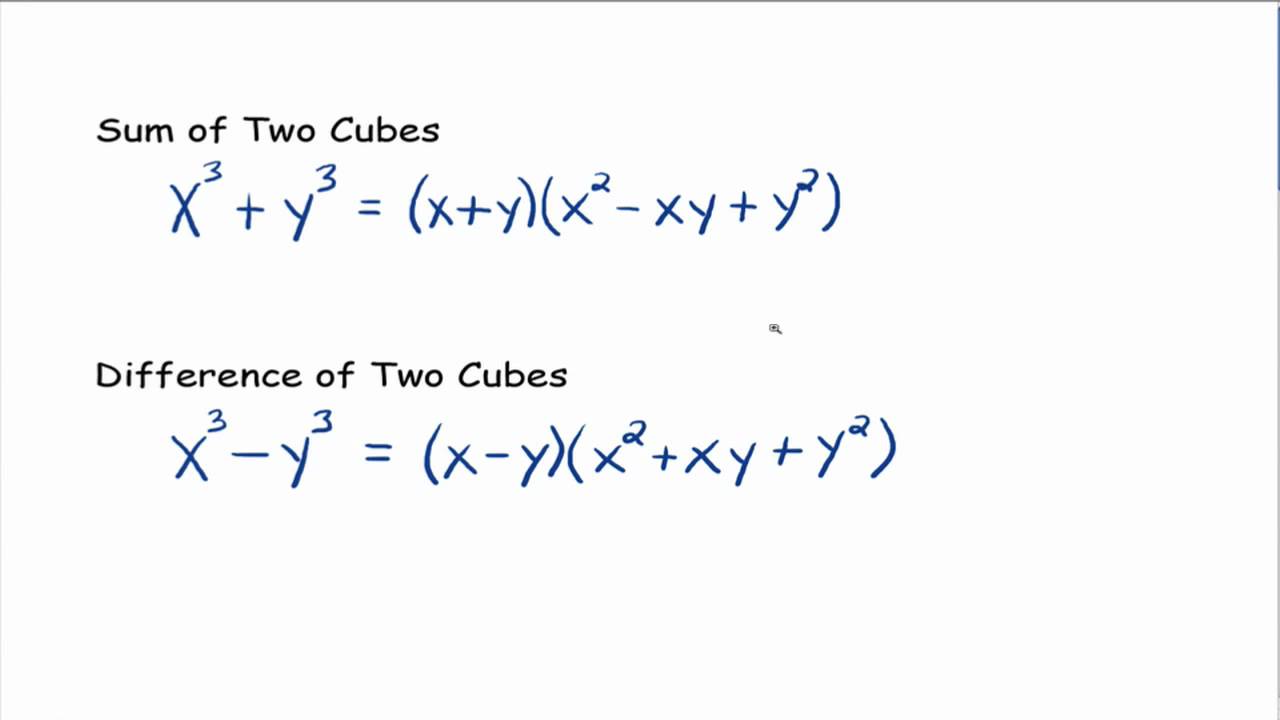How to Break Down a Cubic Difference or Sum It

When you encounter a binomial expression that doesn’t fit the pattern of a difference of squares, you may need to consider whether it’s a difference or sum of cubes. Recognizing and factoring these correctly is essential for simplifying polynomials.

1. Difference of Cubes

A difference of cubes is of the form a3−b3a^3 – b^3a3−b3. This is factored using the following formula: a3−b3=(a−b)(a2+ab+b2)a^3 – b^3 = (a – b)(a^2 + ab + b^2)a3−b3=(a−b)(a2+ab+b2)

2. Sum of Cubes

A sum of cubes follows the form a3+b3a^3 + b^3a3+b3. To factor it, you use: a3+b3=(a+b)(a2−ab+b2)a^3 + b^3 = (a + b)(a^2 – ab + b^2)a3+b3=(a+b)(a2−ab+b2)

Steps for Factoring a Cubic Difference or Sum

Let’s use the example 8×3+278x^3 + 278x3+27 to walk through the process:

Step 1: Look for a Greatest Common Factor (GCF)

Before doing anything else, always check if the terms in the binomial share a common factor. In this case, 8x38x^38x3 and $27$ don’t have a GCF, so we can move on to the next step.

Step 2: Check if it’s a Difference of Squares

You might think this binomial could be factored as a difference of squares, but the plus sign between the terms immediately rules this out.

Step 3: Determine if It’s a Sum or Difference of Cubes

The presence of a plus sign suggests that it may be a sum of cubes. Now, rewrite the terms as cubes: 8×3+27=(2x)3+(3)38x^3 + 27 = (2x)^3 + (3)^38x3+27=(2x)3+(3)3

Since both terms are cubes, it confirms that this is a sum of cubes.

Step 4: Apply the Factoring Formula

Using the sum of cubes formula a3+b3=(a+b)(a2−ab+b2)a^3 + b^3 = (a + b)(a^2 – ab + b^2)a3+b3=(a+b)(a2−ab+b2), replace $a$ with $2x$ and $b$ with $3$:

(2x+3)((2x)2−(2x)(3)+(3)2)(2x + 3)\left((2x)^2 – (2x)(3) + (3)^2\right)(2x+3)((2x)2−(2x)(3)+(3)2)

Step 5: Simplify

Now simplify the expression:

(2x+3)(4×2−6x+9)(2x + 3)(4x^2 – 6x + 9)(2x+3)(4x2−6x+9)

Step 6: Check for Further Factorization

Once you have factored the expression, always check if it can be simplified further. In this case:

• The binomial term $2x+3$ won’t factor any further since it’s a first-degree binomial.
• The trinomial 4×2−6x+94x^2 – 6x + 94x2−6x+9 doesn’t factor any further either.

Thus, your final factored form is:

(2x+3)(4×2−6x+9)(2x + 3)(4x^2 – 6x + 9)(2x+3)(4x2−6x+9)

Frequently Asked Questions (FAQs)

What’s the difference between a difference of cubes and a sum of cubes?

• A difference of cubes has the form a3−b3a^3 – b^3a3−b3 and factors as (a−b)(a2+ab+b2)(a – b)(a^2 + ab + b^2)(a−b)(a2+ab+b2).
• A sum of cubes has the form a3+b3a^3 + b^3a3+b3 and factors as (a+b)(a2−ab+b2)(a + b)(a^2 – ab + b^2)(a+b)(a2−ab+b2).

How do I recognize a cubic expression?

A cubic expression will have terms where the variables are raised to the power of three, such as x3x^3x3, 8x38x^38x3, or $27$ (which is 333^333).

Can I use the same factoring formula for both sum and difference of cubes?

No. The formulas are slightly different:

• Difference of cubes: a3−b3=(a−b)(a2+ab+b2)a^3 – b^3 = (a – b)(a^2 + ab + b^2)a3−b3=(a−b)(a2+ab+b2)
• Sum of cubes: a3+b3=(a+b)(a2−ab+b2)a^3 + b^3 = (a + b)(a^2 – ab + b^2)a3+b3=(a+b)(a2−ab+b2)

What happens if I forget to check for a GCF before factoring?

If you skip this step, you might end up with a factored form that isn’t fully simplified. Always check for a GCF first to ensure your final answer is as simple as possible.

How do I know when I’m done factoring?

After applying the sum or difference of cubes formula, check the resulting factors:

• If the binomial is first-degree (like $2x+3$) and has no GCF, it’s already in its simplest form.
• For the trinomial, check if it fits other common factoring techniques (such as the difference of squares or quadratic formulas). If it doesn’t, you’re done.

Can a sum of cubes ever be factored further?

Generally, after applying the sum of cubes formula, the result is in its simplest form. However, always check for a possible GCF or other factoring methods just to be sure.